Table of Contents
FABRIC FORMED CONCRETE PANEL DESIGN
by Robert P. Schmitz
Robert P. Schmitz, P.E. is a registered professional engineer in the State of Wisconsin, USA with more than thirty-five years experience in architecture and structural engineering. He received his Bachelor of Science degrees in Architecture from the University of Wisconsin-Milwaukee (1973) and Civil Engineering from North Dakota State University (1984) and Master’s in Structural Engineering from the Milwaukee School of Engineering (2004). His research interest in fabric formwork comes as a result of work he completed for his Master’s degree and his desire to see this unique method of forming concrete brought into mainstream construction practice. He is a member of ASCE and ACI. (This paper was written for and presented at the 17th Analysis and Computation Specialty Conference held in conjunction with the 2006 ASCE Structures Congress held in St. Louis, MO)
ABSTRACT
Concrete wall panels have traditionally been cast using a rigid formwork. Straightforward methods of analysis and design are available for the traditionally cast concrete wall or floor panel. This is not so for the panel cast in a flexible fabric formwork. To date, no design procedures or methods to predict the deflected shape of a fabric cast panel have been developed. This paper introduces a design procedure that allows one to design a fabric cast concrete panel.
A four step procedure for analytically modeling a fabric formwork was developed employing the structural analysis program ADINA to analyze the formwork and the concrete panel cast in it. The final panel form, function and performance of the fabric membrane and the reinforcement of the panel for design loads all add to the complexities of the panel’s analysis and design.
Analytical modeling and design techniques presented in this paper will allow members of the design community another way to express themselves using a flexible fabric formwork. No longer will designers feel constrained by the limitations imposed by using a rigid formwork.
INTRODUCTION
BACKGROUND
The use of a flexible formwork appears to be ill suited for casting any concrete member since the way concrete has traditionally been cast has been in an all rigid formwork. However, this method of casting concrete is beginning to attract attention as a method of construction. The author’s first introduction to flexible formwork came from reading an article by Mark West, Director of the Centre for Architectural Structures and Technology (C.A.S.T.) at the University of Manitoba, Canada, published in Concrete International [1]. A visit to C.A.S.T., on the University of Manitoba campus, in June of 2004, brought the author up to date on this state of the art method of construction.
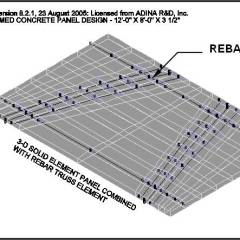
For the past several years, Professor West and his architectural students at C.A.S.T. have been exploring the use of flexible formwork for casting concrete wall panels [2, 3]. The shape a wall panel could take was first explored using a plaster model with various interior and perimeter boundary conditions. The cloth fabric, when draped over interior supports and secured at the perimeter, deforms as gravity forms the shape of the panel with the fluid plaster as shown in Figure 1. Once a satisfactory design has been obtained, a full-scale cast with concrete can be made.
The casting of a full-scale panel using concrete requires finding a fabric capable of supporting the weight of the wet concrete. For this purpose, a geotextile fabric made of woven polypropylene fibers was utilized by C.A.S.T. The flexible fabric material was pre tensioned in the formwork and assorted interior supports were added. Depending upon the configuration of these interior support conditions, three dimensional funicular tension curves were produced in the fabric as it deformed under the weight of the wet concrete. Reinforcement added to the panel, as shown in Figure 2, only served to hold it together and was not designed for any particular loading condition.
The potential benefits for using a flexible fabric formwork include increased freedom of design expression, a design where “form follows function”, economies of construction, and improvement in the finish and durability of the product. Moreover, while a building project may require a wall panel for purely functional reasons, such as resisting the required lateral loads and keeping the weather out, aesthetic reasons may require these panels to be expressive in the form they take. From an engineering perspective, however, the challenge remains of finding a method to analyze the complex structural shape a wall panel could ultimately take.
Proposed Design Procedure
This paper presents a procedure developed in the author’s graduate Capstone Project that allows one to design a fabric cast concrete panel [4]. A four step procedure for analytically modeling the fabric formwork, loaded with the plastic concrete, was developed in order to determine the final shape of the concrete wall panel and analyze it. These steps are:
- Determine the paths the lateral loads take to the points where the wall panel is to be anchored.
- Use the load paths, defined in Step 1, to model the fabric and plastic concrete material as 2-D and 3-D Solid elements, respectively. These elements are arranged to define the panel’s lines of support.
- “Form find” the final shape of the panel by incrementally increasing the thickness of the 3-D Solid elements until equilibrium in the supporting fabric formwork has been reached. This process is equivalent to achieving a flat surface in the actual concrete panel.
- Analyze and design the panel for strength requirements to resist the lateral live load and self weight dead load being imposed upon it.
By utilizing the above four step procedure, it is expected that obtaining an optimal panel shape is possible. The implication is that the above procedure becomes an iterative process. If, after an analysis of the panel is made in Step 4, it is found that the panel is either “under strength” or too far “over strength”, adjustments to the model in Step 2 will be required and Steps 3 and 4 repeated. Prior to implementing this four step procedure, however, the modeling techniques utilized in Steps 2 and 3 above must first be defined.
ANALYSIS METHODOLOGY AND MATERIALS
Finite Element Analysis (FEA) Model Development
Model development and analysis of the fabric cast concrete panel is performed utilizing the structural analysis/finite element program ADINA [5, 6]. Efficient modeling plays an essential role in the development of this finite element model. The elements making up the supporting fabric formwork and the elements, which eventually make up the final concrete panel shape, are defined in the same model. Once the final concrete panel shape is defined by using an iterative “form finding” technique, the fabric elements are discarded. The concrete panel elements are then designed for the appropriate lateral loads under the given set of boundary conditions. While a surface load defined by a “quadratic surface spatial function”, representing the weight of the concrete, could be used to find the shape of the panel using the same iterative procedure, it would not be as efficient as the proposed method – and defining element nodal locations would be extremely difficult and time consuming.
The difficulty with combining the two element types required to define the overall model is that they each have their own material properties, which can contribute to the overall strength and stiffness of the model. Initially, the concrete is plastic and is considered fluid in nature, similar to slurry. The slurry will contribute weight to the fabric element portion of the model but cannot contribute stiffness to it. Therefore, an intermediate step is required. In this step, the slurry – characterized as a material that has weight, but no strength or stiffness – is used as the material property for the concrete panel elements while the panel shape is being found.
The Fabric Model and Material Properties
Advantages of Geotextile Fabric as Formwork Material include:
- Very complex shapes are possible. Designs are limited only by one’s imagination.
- Geotextile fabric is strong, lightweight, inexpensive and reusable.
- Less concrete and reinforcing are required resulting in a more efficient design.
- Improved surface finish and durability of the concrete product are possible due to the filtering of air bubbles and excess bleed water through the fabric.
Disadvantages include:
- Relaxation can occur due to the prestress forces in the membrane. There is the potential for creep in the geotextile material, which can be accelerated by an increase in temperature as might occur during hydration of the concrete as it cures.
- The concrete must be placed carefully and the fabric formwork must not be jostled while the concrete is in a plastic state.
Material Properties of Geotextile Fabrics
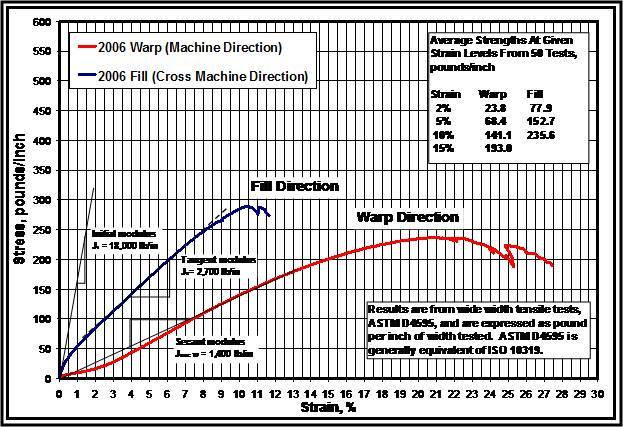
The material is anisotropic. The modulus of elasticity is different in the WARP (machine direction, along the length of the roll) and the FILL (cross machine direction, through the width of the roll). These differences are important when modeling the fabric as well as for securing it to the supporting formwork. Mechanical properties for geotextile fabrics are obtained from stress strain curves developed in accordance with the standard test methods of ASTM D4595 [7]. A stress strain curve is required for each direction of the material. Depending upon the appearance of the material’s stress strain curve, a determination is made whether a Hookean (linear) region exists or not. Based on this determination the initial, tangent and offset (or secant) tensile modulus may be constructed.
| TABLE 1 | AMOCO 2006 GEOTEXTILE FABRIC MATERIAL PROPERTIES |
|---|---|
| t = 0.03-in | Fabric thickness |
| Ewarp = Ea = 46,667 psi | Modulus of Elasticity, Machine Direction |
| Efill = Eb = 90,000 psi | Modulus of Elasticity, Cross Machine Direction |
| G = 23,333 psi | Shear Modulus |
| v = 0.0 | Poisson's Ratio |
Stress strain data for the Amoco 2006 geotextile fabric, the material being modeled, was obtained from Amoco Fabrics and Fibers Company [8]. Figure 3 shows the stress strain curves resulting from tests conducted by Amoco, and using the appendixes of ASTM D4595 as a guide, the author has constructed the initial, tangent and secant tensile moduli. Information obtained from Figure 3 allowed the properties shown in Table 1 for this elastic orthotropic material to be entered into the ADINA material model. There is little interaction between the two perpendicular directions in a woven fabric and a value of zero for Poisson’s Ratio was chosen for this material model [9].
Relaxation and Creep in Geotextile Fabrics
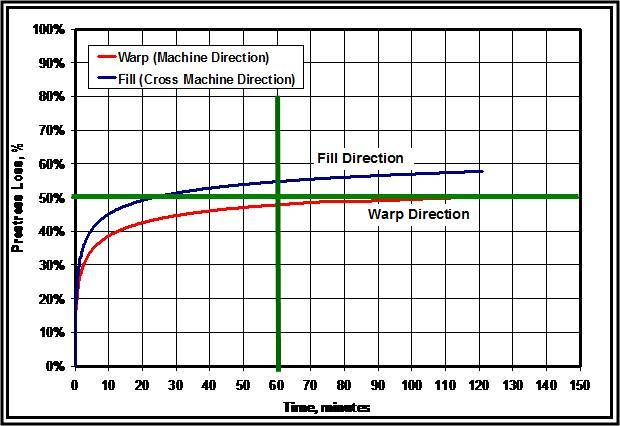
The effects of creep in the geotextile fabric are not included in this paper but relaxation will be considered in the modeling of the fabric panel. Loss of prestress due to relaxation of the fabric can exceed 50% after just a 20-minute period depending on the percentage of initial prestress and the direction in which the fabric is prestressed. Figure 4 shows the percent loss in prestress from relaxation tests conducted by AMOCO in the WARP and FILL directions with the fabric prestressed to 2%.
Geotextile fabrics are temperature sensitive, and as a result, creep as the temperature increases [11]. Creep may be more of a factor as the concrete panel cures due to the heat of hydration than initially as the concrete is being poured into the fabric formwork. (See an animation of a concrete panel going through temperature changes during the initial curing cycle on the ANIMATIONS page.)
ADINA Fabric Model
The ADINA computer model representing the supporting fabric formwork uses 9-node, 2-D Solid elements. The 2-D Solid element uses a 3-D plane stress (membrane) kinematic assumption.
A prestress load of 2% is applied to the fabric in the cross machine direction with a 50% reduction in the modulus of elasticity, Eb, due to relaxation, assuming the concrete is poured within one hour of prestressing the fabric. A one half percent prestress load is applied in the machine direction to keep the fabric taut with no reduction in Ea being taken. Thus, the modulus of elasticity is approximately equal in each direction. The initial stresses in the fabric, due to these prestress loads, are found by
σa = Ea εa = 233.3 psi (Machine Direction)…………………(1)
and
σb = 0.50 (Ebεb) = 900.0 psi (Cross Machine Direction)…..(2)
where
Ea Modulus of Elasticity in the Machine Direction,
Eb Modulus of Elasticity in the Cross Machine Direction,
εa strain in the Machine Direction (due to prestress load),
εb strain in the Cross Machine Direction (due to prestress load).
The Slurry Model and Material Properties
The ADINA computer model representing the slurry material will use 27-node, 3-D Solid elements. The slurry material, as stated above, must not contribute stiffness to the fabric element portion of the computer model. As a result, a very low modulus of elasticity must be used for this elastic isotropic material. The slurry material will function as the load on the fabric element model using the slurry’s density as a mass proportional load. Table 2 summarizes the slurry material properties used in the ADINA material model.
| TABLE 2 | SLURRY MATERIAL PROPERTIES |
|---|---|
| t = varies-in | Slurry thickness |
| E = 2 psi | Modulus of Elasticity |
| vsm = 0.0 | Poisson's Ratio |
| wtsm = 145 lbs/ft3 | Weight |
| Dsm = 0.00021716366 lb-sec2/in4 | Density |
PANEL DESIGN AND OPTIMIZATION
The design of a fabric formed concrete panel may be approached several ways. Each approach must take into account the panel’s anchor locations to the backup framing system. One approach might be to locate the anchor points based on the most efficient panel design. Another approach could locate the anchor points based on the most pleasing appearance the panel takes due to the deformed fabric shape, and still another could consider both efficiency and appearance as a basis for the anchor locations. The variables, which could be subject to adjustment, assuming a plain concrete design is utilized, are:
- Concrete strength
- Initial panel thickness
- Prestress in fabric formwork and
- Anchor locations
For demonstration purposes, a 12’-0” long x 8’-0” wide x 3½”–thick panel, formed over a fabric formwork prestressed to 2% across the panel length and one half percent across the panel width, will be designed for self weight and a ±30 psf lateral wind load using a concrete strength of 5,000 psi.
The fabric in this model will be laid with the cross machine direction spanning the narrow dimension of the panel. The fabric in the machine direction, along the length of the panel, will be prestressed just one half percent to keep it taut. It should be emphasized here that the direction the fabric spans and the variables listed above can all come into play depending on the panel design requirements.
With the fabric formwork modeling techniques defined, the four step procedure outlined above may now be used to design a fabric formed concrete panel. A first step in obtaining an optimum panel design requires that the load paths to the boundary supports be determined – a result of the lateral loads. The anchors are then placed at these locations anchoring the panel to the backup framing system. If, for architectural reasons, the panel is to be configured with predetermined load paths and anchor locations, this step could be omitted.
Step 1 – Determination of Load Paths
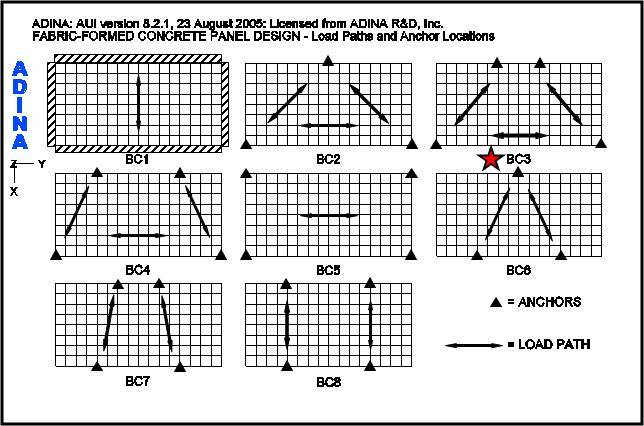
In the first step, a study of a uniformly thick panel with various boundary conditions is performed in order to determine the load paths an applied lateral load might take. A distributed unit load is applied to a series of panels using 3-D Solid elements and an examination of the principal stresses is made. For this study, any uniform material type may be used. Figure 5 shows the results of these panel investigations for a variety of boundary conditions. The general direction the maximum principal stresses take is indicated by the double headed arrows.
Note in Figure 5 that panel anchor locations appear to result in load paths, which fall into one of two cases. Load paths defining Case 1 are parallel to one of the panel’s edges as shown in Panel BC1, which has a continuous simple edge support, or Panel BC5 and Panel BC8, which have symmetrical 4-point anchor locations. The load paths in the remaining panels appear to triangulate in their direction between the anchor locations and define Case 2. For demonstration purposes, the anchor locations shown in Panel BC3 are assumed – where the load paths triangulate. This anchor arrangement was also chosen for the interesting shape the final panel design takes.
Step 2 – Define Fabric Formwork Design
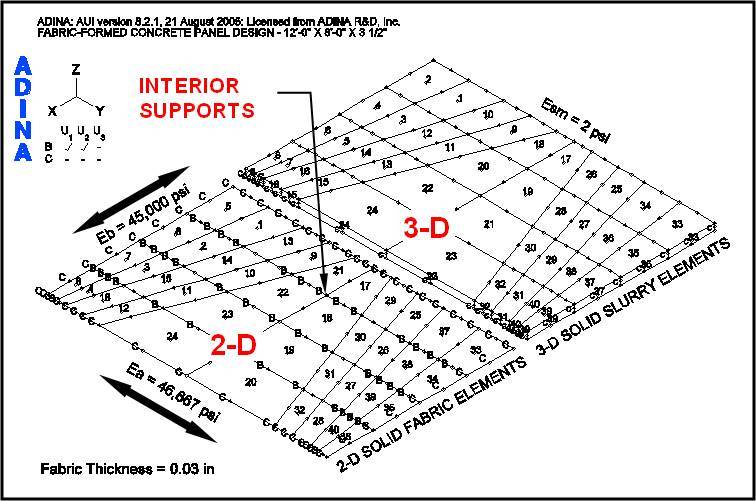
Based on the study of the load paths shown in Figure 5, the formwork is laid out and the interior and perimeter boundary conditions are introduced as shown in Figure 6. Interior supports are indicated by a “B” in this figure. The fabric will deflect between these interior supports creating thicker panel regions – capable of resisting more load than at the supports where it remains at its initial thickness. These deflected regions define the panel’s load paths. Increased strength will be provided spanning the width of the panel along a diagonal path, for a 4-point anchor condition, due to these thickened regions. In addition, “collector” paths are formed along the length of the panel to bring the load to the diagonal load paths.
Step 3 – “Form finding” the Panel Shape
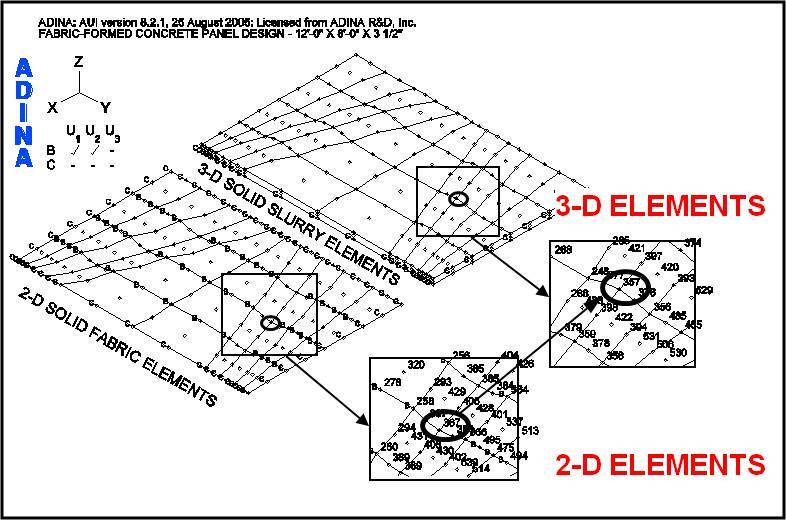
The ADINA model represents the supporting fabric formwork in combination with the slurry material, which functions as the load on the formwork. Figure 6 shows the 9-node, 2-D Solid fabric elements and the 27-node, 3-D Solid slurry elements in the ADINA model. For clarity, the fabric and slurry element groups are shown separately.
The 2-D Solid fabric elements are prestressed 2% in the cross machine direction, one half percent in the machine direction and use a large displacement/small strain kinematic formulation. To be consistent with the 2-D fabric elements, the 3-D slurry elements also use the large displacement/small strain kinematic formulation.
Now that the model is defined, “form finding” of the panel shape may proceed. Initially, the 3-D slurry elements are uniformly 3½-in–thick. “Form finding” the panel shape proceeds as follows:
- Run the model under slurry gravity loading and determine the interior fabric element node displacements.
- Increase the 3-D element thicknesses at each interior node (e.g., at node 357, Figure 7) by the amount the fabric displaces (e.g., at node 367, Figure 7). The bottom node remains stationary while the top and mid level nodes are adjusted upward. (The computer model panel is formed in reverse of how it would occur if the slurry were actually being poured into the fabric formwork.)
- Rerun the model and determine the interior fabric element node displacements.
- Repeat Steps 2-3 until displacements between the last two runs are within a tolerance of approximately 1%.
Given the hundreds or even thousands of interior nodal locations that will require adjustment, depending on the size and complexity of the model, the task of manually adjusting the nodal locations becomes daunting. Fortunately, ADINA can both output displacement information and input nodal locations using text files, which when used with a spreadsheet program greatly facilitates this “form finding” task. Still, what would be desirable is a program that can automatically update its nodal locations. (See an animation of a concrete panel going through the form-finding process on the ANIMATIONS page using ANSYS.)
The finite element model in Figure 8 shows the results of “form finding” the panel shape made up of the slurry material. The boundary conditions that created it are illustrated in Figure 6.
Step 4 – Panel Analysis and Design
A strength analysis of the panel will need to be performed before any judgment can be made of whether or not the panel is adequate. The panel design may be optimized, to account for over or under strength, by adjusting the variables noted above and repeating Steps 3 and 4 of the design procedure.
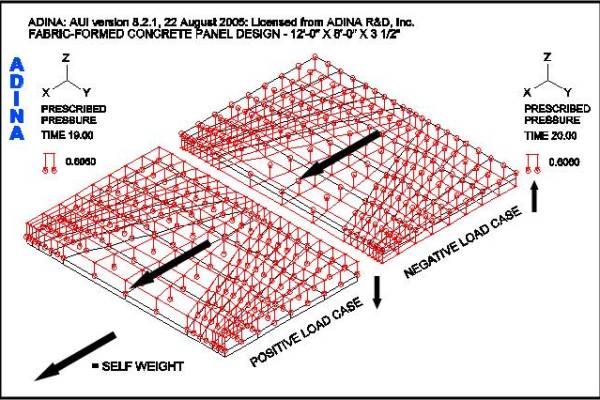
The panel shape defined in Figure 8 may now be analyzed for strength under the ±30 psf design lateral wind load and gravity self weight. The lateral loads will cause bending in the panel and the gravity loads are in plane loads that will contribute to membrane action in the vertically oriented panel. Two lateral load cases are considered; a positive load case and a negative load case as shown in Figure 9. The panel will be analyzed using the strength design method for plain concrete and ACI 318-02, Section 22 [12]. The required factored loads are
PuD = 1.2 x Dc………………………(3)
and
PuW = 1.6 x 30 psf = 48 psf………..(4)
where
Dc Density of concrete panel,
PuD Factored dead load,
PuW Factored wind load.
| TABLE 4 | CONCRETE MATERIAL PROPERTIES | TABLE 5 | REINFORCING MATERIAL PROPERTIES | |
|---|---|---|---|---|
| t = varies-in | Concrete panel thickness | Es = 29,000,000 psi | Young's Modulus of Elasticity | |
| Ec = 4,074,281 psi | Secant Modulus of Elasticity | Ets = 290,000 psi | Strain hardening (Tangent) Modulus | |
| Etc = 7,129,991 psi | Initial Tangent Modulus of Elasticity (Assume 1.75 x Secant Modulus) | fy = 60,000 psi | Initial yield stress | |
| f΄c = 5,000 psi | Compressive strength of concrete (SIGMAC) | Ds = 0.0007339 lb-sec2/in4 | Density | |
| εc = 0.002 | Compressive strain of concrete at SIGMAC | |||
| f΄uc = 4,250 psi | Ultimate compressive strength of concrete (SIGMAU, assumed @ 85% f΄c) | |||
| εuc = 0.003 | Ultimate compressive strain of concrete at SIGMAU | |||
| fr = 5√ f΄c = 353.6 psi | Uniaxial cut-off tensile strength of concrete | |||
| νc = 0.20 | Poisson’s Ratio | |||
| wtc = 145 lbs/ft3 | Weight | |||
| Dc = 0.00021716366 lb-sec2/in4 | Density | |||
| Φp = 0.55 | Strength reduction factor for plain concrete |
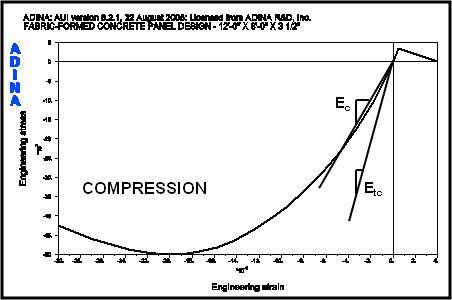
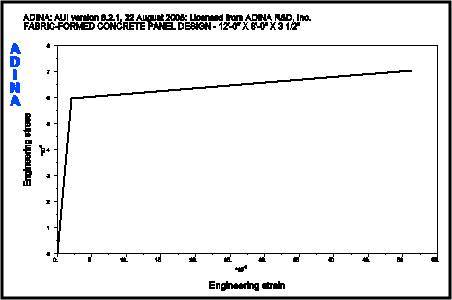
The properties for the slurry material are now replaced with the properties for concrete. Table 4 summarizes the concrete material properties used in the ADINA material model. Where the panel is reinforced, model material properties for the reinforcing steel are summarized in Table 5. Stress strain curves for the concrete and reinforcing steel are shown in Figures 10 and 11, respectively.
The governing criterion for structural plain concrete design is the uniaxial cut off strength of the concrete or Modulus of Rupture as stated in Section 22 of ACI 318-02. Maximum principal tensile stresses resulting from positive and negative wind loads combined with gravity loads must fall below this value, which for 5,000 psi concrete is 353.6 psi. When the maximum principal tensile stress is greater than the Modulus of Rupture, the ADINA model indicates this point by a “crack” in the panel model. The ADINA Theory and Modeling Guide notes: “…for concrete…. these are true principal stresses only before cracking has occurred. After cracking, the directions are fixed corresponding to the crack directions and these variables are no longer principal stresses” [6]. ADINA uses a “smeared crack” approach to model the concrete failure. Following are summary graphic output and results for the panel under investigation.
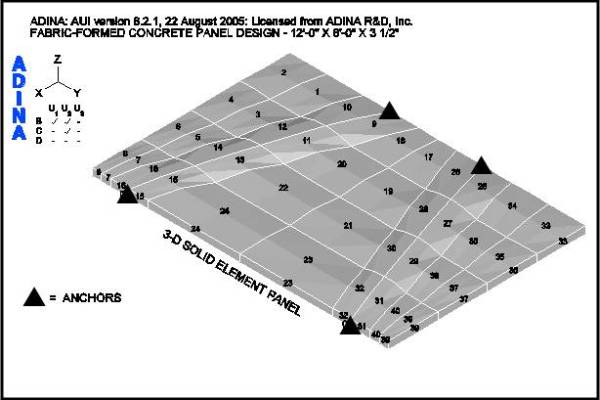
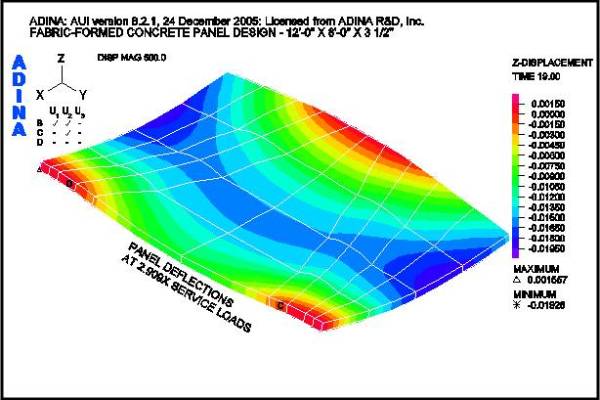
Figure 12 shows the FEA model for the panel under consideration. Positive and negative load cases as shown in Figure 9 are considered. The finite elements are arranged in a pattern that follows the fabric formwork design shown in Figure 6 and are supported with a 4-point anchor arrangement. After “form-finding”, the final weight of the panel is 4,941 lbs. Figure 13 shows the deflected shape under the factored positive load case. The maximum service load deflection is 0.0066-in.
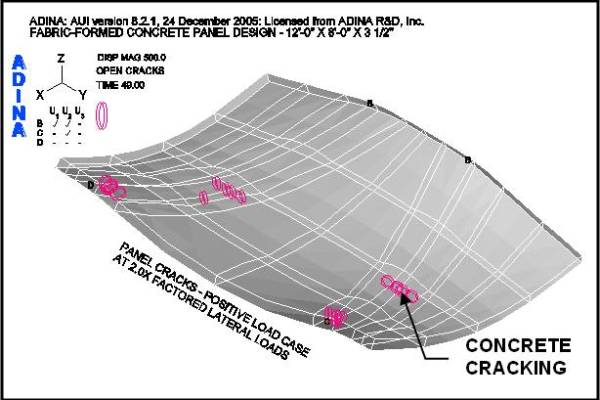
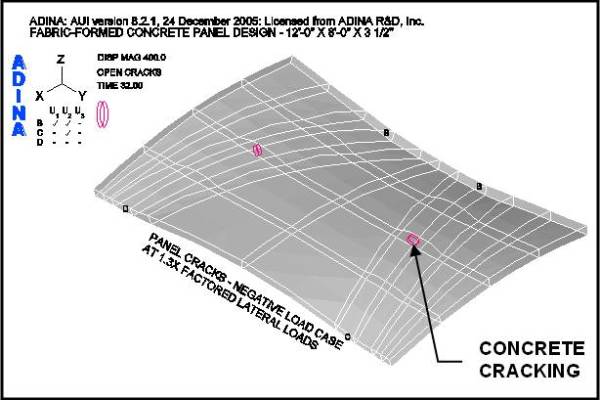
Figures 14 and 15 show the loading conditions under which the panel first cracks. For case two, the negative load case, the first cracks occur at 1.3-times the factored load as shown in Figure 15. For case one, the positive load case, the panel does not crack at the factored load. Cracks, within the body of the panel, do not occur until 2-times the factored positive load is reached, as shown in Figure 14 – local cracking at the supports being ignored.
Figure 16 shows a maximum principal tensile stress of 193 psi for the positive lateral load case at the factored load. Figure 17 shows the maximum principal tensile stress of 289 psi for the negative lateral load case at the factored load. Load paths between the supports are indicated by the double headed arrows. This corresponds to the load path for Panel BC3 shown in Figure 5. This panel has a maximum thickness of 5.89 in and an equivalent uniform thickness of 4.26-in. It has achieved an optimal form with its final shape remaining the same as its shape after “form-finding” shown in Figure 8.
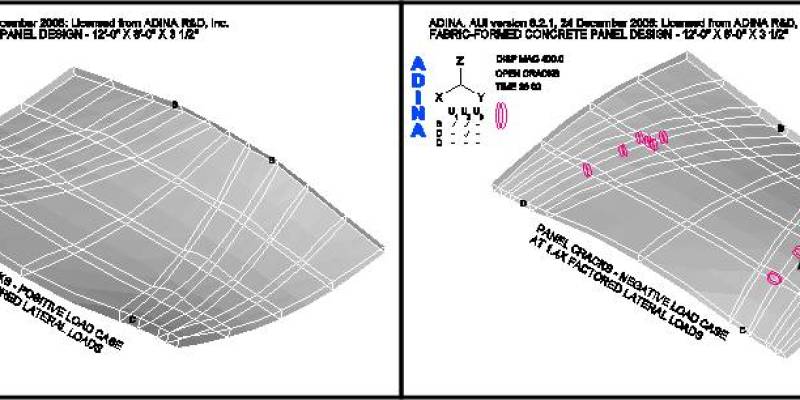
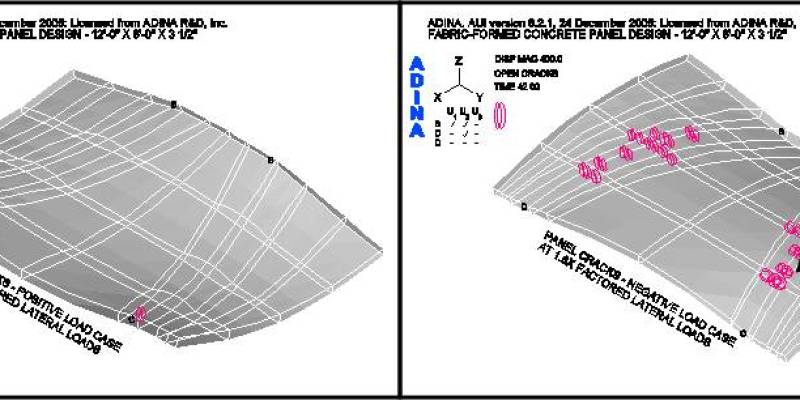
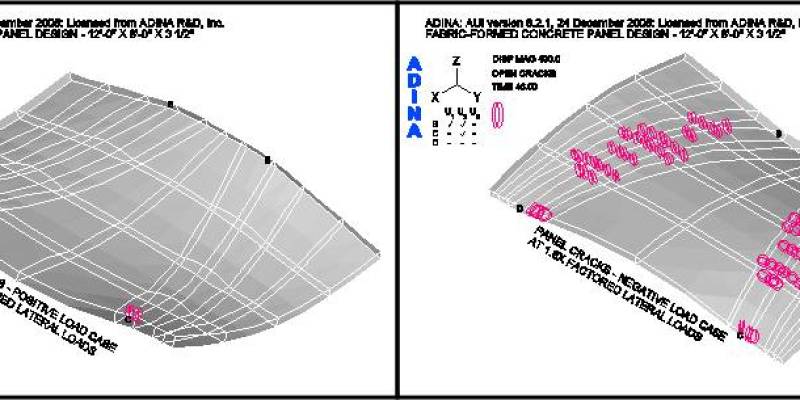
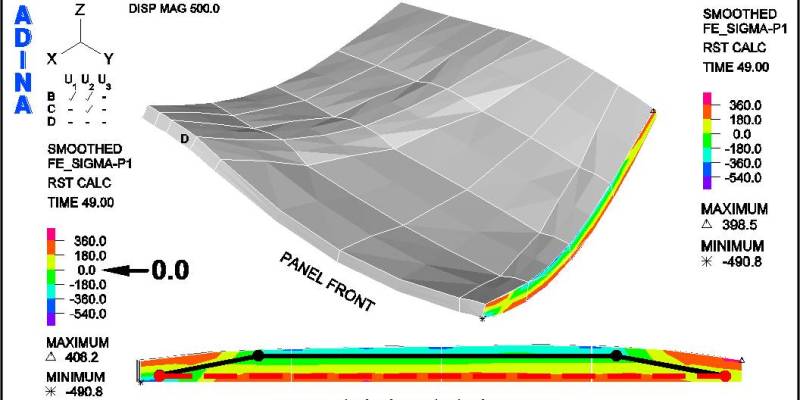
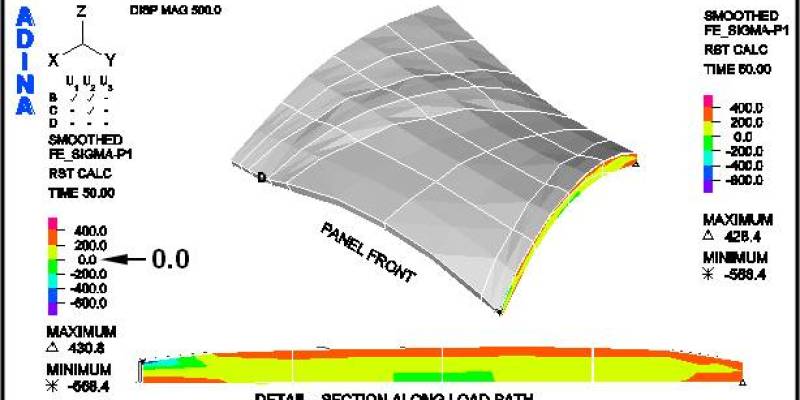
Figure 18 shows the crack patterns that occur as the panel is loaded past the factored lateral design loads for both load cases. It may be observed that under the positive lateral load case the panel does not crack, within the body of the panel, as the load is incrementally increased from 1.4 to 1.8 times the factored positive load. However, under the factored negative lateral load case, the panel shows progressively more cracks as the load is increased. This series of figures clearly shows the benefit of the funicular tension curves, in the fabric formwork, which produced this panel shape. (See an animation of a concrete panel as it cracks while going through cyclic loading on the ANIMATIONS page.)
Figures 19 and 20 show tensile and compressive principal stress at a section cut along the diagonal load path. Figure 19 shows the effect of arching action similar to a strut and tie model under the positive lateral loads. Compressive forces in these curved panel elements, created under the positive lateral load, allow the panel loads to be steadily increased without the interior of the panel cracking. Conversely, under the negative lateral load case the benefit is not observed, as shown in Figure 20, where the principal stresses are mostly in tension. Reinforcing would be required if additional load capacity were desired.
Reinforcement Considerations
The results of a plain concrete analysis for the panel under consideration show that a minimum panel thickness of 3½-inches is adequate. Figure 21 shows one possible reinforcement arrangement should some or all the variables noted above be exhausted and the only way to achieve an adequate panel design is to reinforce it. The reinforcement is placed where the principal tensile stresses are greatest.
CONCLUSIONS AND RECOMMENDATIONS
Conclusions
The procedures introduced in this paper are useful in the analysis and design of a flexible fabric formwork and the resulting complex concrete panel shape thus formed. The slurry material used with the 3-D Solid finite element proves very useful in saving FEA modeling time by allowing the panel shape to be formed and then later analyzed by simply substituting a concrete material model for the slurry material model without remeshing the FEA model.
The computer program ADINA is well suited to analyze the complex shape a fabric formed concrete panel can take. In addition, it is capable of utilizing the different material models required at each step of the design process.
Recommendations
The advancement of fabric-formed concrete member design would be furthered by implementing the following list of research topics:
- The development of computer software, which would automatically “form-find” the panel shape and then allow it to be analyzed, is needed. Manual methods utilizing spreadsheet programs are feasible for only very small models.
- Design verification by analysis and testing of full-scale wall panels needs to be performed.
- The role creep plays in the geotextile fabric formwork during the design process needs to be determined.
- Reinforcement options such as fiberglass rebar and alkali resistant (AR) glass textile need to be investigated in concrete panel design.
ACKNOWLEDGMENT
The author wishes to express his sincere appreciation to Professor Peter Huttelmaier, Ph.D. who served as Capstone Project advisor during graduate studies at the Milwaukee School of Engineering and offered insightful and constructive comments during the preparation of this manuscript. In addition, special thanks go to Professor Mark West, Director of the C.A.S.T. at the University of Manitoba, whose work on fabric-cast concrete wall panels provided the inspiration for this project. The author also wishes to thank Geri Schmitz and Gary Shimek, MLIS for their efforts in proofing this manuscript.
See Also
References
[1] West, Mark. October 2003. “Fabric Formed Concrete Members.” Concrete International Vol. 25(10), pp. 55+.
[2] West, Mark. April 2002. “Fabric Cast Concrete Wall Panels.” Materials Technology Workshop, Department of Architecture, University of Manitoba, Canada. [Internet, WWW]. Address: http://www.umanitoba.ca/cast_building/resources.html
[3] West, Mark. April 2004. “Prestressed Fabric Formwork for Precast Concrete Panels.” Concrete International Vol. 26(4), pp. 60+.
[4] Schmitz, Robert. 2004. “Fabric Formed Concrete Panel Design.” Master’s thesis, Milwaukee School of Engineering, Milwaukee, Wisconsin 53202.
[5] ADINA R & D, Inc. September 2004. ADINA (Version 8.2.1). [Computer program]. Available: ADINA R & D, Inc., 71 Elton Avenue, Watertown, Massachusetts 02472.
[6] ADINA R & D, Inc. September 2004. ADINA – Theory and Modeling Guide. Report ARD 04-7. Watertown, Massachusetts: ADINA R & D, Inc.
[7] ASTM International. ASTM Committee D35 on Geosynthetics. 2001. Test Method for Tensile Properties of Geotextiles by the Wide Width Strip Method, Designation: D 4595-86 (Reapproved 2001). In Annual Book of ASTM Standards 2001. Vol. 4.13: Geosynthetics. West Conshohocken, Pennsylvania: ASTM International, pp. 1-10.
[8] Baker, Thomas L. 2002. Amoco 2006 Stress Strain. Atlanta, Georgia: Amoco Fabrics and Fibers Company. [Internet, e-mail to the author].
[9] Soderman, K.L. and J.P. Giroud. 1995. “Relationships Between Uniaxial and Biaxial Stresses and Strains in Geosynthetics.” Geosynthetics International Vol. 2(2), pp. 495-504.
[10] Baker, Thomas L. 2005. Amoco 2006 Relaxation Results. Atlanta, Georgia: Amoco Fabrics and Fibers Company. [Internet, e-mail to the author].
[11] Terram Ltd., May 2000, “Designing for Soil Reinforcement (Steep Slopes),” Handbook, (United Kingdom: Terram Ltd.), pp. 19-22. [Internet, WWW]. Address: http://www.terram.co.uk
[12] ACI Committee 318. 2002. Building Code Requirements for Structural Concrete (ACI 318 02) and Commentary (ACI 318R-02). Farmington Hills, Michigan: American Concrete Institute.